|
From the point of view of a design engineer there is within the artificial neural network literature a bias which in a certain way restricts ideas, and which has the effect of suppressing some types of valuable development. This sort of difficulty is not confined to the field of artificial neural networks, but it is interesting to develop the idea in this context because there seem to be good examples of some simple but valuable types of artificial neural network which have been neglected as a result of this inhibition.
This problem is rooted in the basis of assumptions and habits underlying the rational approach to the work. This is of interest from a cybernetics point of view in that we need to be aware of how to handle models within the processes of change and innovation.
After some discussion of the thought processes involved, particularly in the prospective design of such systems, this paper develops a model like a Fokker-Planck equation to characterise the statistical behaviour of a class of neurons which perform an unsupervised adaptation for the mapping of input vectors to a self selecting symbol code space.
Anthony G Booth 1995 |
Anthony G Booth | 3 November 1995 |
| ** Introduction. | Why "Minimal"? | |
| ** The Developing Paths. | Some Constraints on Development. | |
| ** Routes to New Mental Models. | Relaxing the Determinist Stance. | |
| ** Objectivity and the Scientific Method. | A Need for Local Models. | |
| ** Contentions, both conscious and not. | ..... in both Humans and Machines. | |
| ** Unsupervised Learning. | Weaknesses of the usual Global Viewpoint. | |
| ** Method. | ||
| ** To Deduce is not to Educe. | Deduction alone is not enough. | |
| ** Localisation in New Abstract Spaces. | Opportunities for New Synthetic Structures. | |
| ** Results. | ||
|
** More Abstract Space from Less Neuron Function. | Analysis of the Neuron Model. | |
| ** Discussion and Conclusion. | ||
| ** Critical Points of Neuron Structure. | Design Options and Problems of the Neuron. | |
| ** Acknowledgements. | ||
| ** References. |
Why "Minimal"?
The word "minimal" in the title may need clarification. It is not meant to suggest that we might merely avoid analysis or that we should take a cavalier attitude to careful thinking. Rather it is concerned with the way we choose and view our analytical models so as to minimise the commitments we make whilst maximising the ongoing options and opportunities. It is concerned to yield a new situation which when looked back upon appears simple and practical, even though we are working in a complex system.
In complex situations the objective can be hindered by insistence solely upon rigorous application of old models. Even if heavy apparatus of thought and argument is employed to clear the ground during early work, it does not mean that this same apparatus is a good basis for clarification and ongoing development. Nor does it mean that the completion of a rigorous proof signifies power of the argument in a broader context. This is because rigour works within a context, whereas definition or redefinition of context is often required for simplification of a new situation. The choice of models and how they are applied is of crucial importance, and at its root that is not analytical work. This is an essential concern at the heart of science and of engineering design.
In this particular frontier aspect of innovative endeavour personal inspiration counts for a great deal, and deductive reasoning is of no direct help because deduction can never shift its own paradigm of operation. Thus to move beyond a total and naive reliance upon such personal inspiration the only remaining option is to develop a communal approach with some sort of dialectic process. Ironically there is a prospect for computing machines, and particularly self-adaptive ones, to help in this process.
When using the approach of the so called "artificial intelligence" (or at least, the "cognitivist" variety [VTR91]) the structure of the perceived problem in symbolic terms is usually made the main issue, but here we consider the prospect of making machines which can apply originality on a general basis to large quantities of micro-problems which have never reached the level of human perception. Such an approach to problem solving is very different from the conventional sense of cognitivist artificial intelligence as operation by rules upon given symbols, although it does not go so far as to exclude symbols from the model totally. It is more concerned with how a machine might itself assign and maintain symbols within a problem domain in a manner not economically accessible to the designer or the practically limited observer. It is minimal in the sense that it seeks only to work in depth on the most abstract generalities of mechanism for identifying things, not on the synthesis of logical machines to solve problems with structures which are already identified consciously by humans.
This little explored approach to neural synthesis stands to strengthen our understanding of the elements of original cognition. Also in the development of helpfully adaptive machines such mechanisms are needed before the mass handling of "micro-problems" too detailed to command explicit human attention can even begin. This might be thought of as a "machine sub-conscious".
This paper arises as the consequence of the author's interest in certain aspects of neural network developments over a number of years. Its special interest is in the fringe of the work which takes it into new sorts of design and description, rather than in an approach using stacked up or powerful older arguments. It is driven by the sense that little of the massive amount of work recently devoted to neural networks has been effective in making the transition beyond a globalist or determinist framework of thought. Though the subject is fascinating, this is not motivated by a mere dilettante sense of contrariness to amuse the engineering mind nor by raw mystical escapism, but rather it is the result of a conviction that work in this direction offers opportunities for some genuine extension of the technological experience in both practice and psychology.
Some Constraints on Development.
Much work was done during the nineteen eighties on artificial neural networks. In spite of this high volume it followed certain rather selective lines. It is a complicated pattern but some broad lines relevant here are visible.
One factor of selection lay in a preference for:
a) Adherence to classical models and global performance measures.
In this sense earlier work in the decade based upon physical metaphors of causal networks pursued some very specific forms (such as Boltzman machines) or linkages amenable to certain laws of reciprocity or Hamiltonian mechanics (like Hopfield nets) which lead to rather specific fields of application (for a review refer to [Hay94]). Even recent work around 1990 using an information theoretic basis (the use of principal components analysis features strongly) still appears to hold fast to measures of correlative performance considered for a whole neuron or even whole network, whereas models of signal ensembles in limited regions of the signal space though less globally objective in nature would often be of more direct help in comprehension and assessment of the value of a component in a system.
Wherever a least mean square error criterion is applied across the entire function of some physical element this narrowing influence arises. It implicitly presumes that an adequate model of the signal is the unstructured linear superposition of temporally incoherent terms and it does not take advantage of any redundancy in the compound domain of vector space and time together. That presumption neglects the substantial power and simplicity of processing which is possible for signal vectors of a sufficient order (tens to hundreds) if they are made up of temporally sparse superposed groupings of underlying terms. To take advantage of this we must move beyond the global model without losing all sense of direction amongst a plethora of wild and peculiar structures.
Further, in many cases there appears to have been a restriction engendered through familiarity with conventional electronic machines and neuro-biological notions leading to:
b) Adherence to existing notions of signal processing machine elements.
In this sense much of the work of the early eighties was constrained to notions of mechanism taken rather naively from existing network principles such as the raw concept of the McCulloch-Pitts neuron. Also the idea of a machine as being deterministically programmed seems to have caused a concentration of work in the earlier part of the decade upon supervised learning (for example back propagation dealing with the inherent need for communication when applying supervision).
The lesser remaining volume of work in that period which was devoted to unsupervised adaptation held firmly to mapping the notion of an emergent identifiable mode in a machine to a physical point in a network (practically entirely following the long term initiatives by Kohonen in the specific form of two dimensional feature nets, which is also reviewed in [Hay94]).
The proposal contained in this paper is not opposed to the development of objective and global measures and models for use where applicable, nor to work on interesting special structures however specific. However, it does attempt to highlight how potential developments in this field have been delayed or hidden by these constraints. It is possible that broader and more valuable results might have been achieved for the same effort. The notes by W.Atmar [Atm94] seem to move in a sympathetic direction of thought, but there the concern is with the somewhat different field of genetic algorithms. The occasional comments regarding neural processes in that paper are not developed and are sadly even a little negative. The works of Varela and Maturana are central references for these developing ways of thinking. The recent book by Varela et al [VTR91] gives a bold and general overview of such ideas.
Can we find a more direct path to radical forms of models by identifying the nature of what can constitute new cybernetic models? How might this be introduced either into the possible forms of mechanism, or alternatively into the way we think of such mechanisms?
Let us first take a general look at this sort of conceptual difficulty.
Relaxing the Determinist Stance.
There is at large an intellectual habit of rational determinism, probably stronger in the culture of the Euro-western world. It links to the exclusive belief in an objective view of causal reality. This habit is good for consolidating models, but resists the formation of new ones. This influence is so strong that it seems to cause an unsuitable bias in approach to work on artificial neural networks. It leads to global analysis using existing models instead of the seeking of useful ways of making it possible to re-assess situations on a local and relevant basis, be that by either a machine or a designer. The problem with this is that it brings about interactions between issues which otherwise are not or need not be related.
In the structures of our models of artificial information mechanisms we must not expect that the characterisation of the machine can be total, but rather that such a mechanism can operate in a space of its own reality which is not fully grasped by us. We might compare this metaphorically with how a farmer thinks of his crops growing, though with the way farming has gone recently it appears that this idea is often lacking there too!
In the domain of the process of human expression of models for these mechanisms we must not expect that existing models can be merely extended by addition of detail to meet the new requirements.
In attempting to deal with complex system design we must not merely labour to make a new device by constraining it to meet a given purpose, but seek rather a refinement of the basic sense of mechanism to be elegantly sparse and hence easy both to understand and to apply in general ways. In the case of minimalist thinking the idea is taken perhaps a little further in making a virtue of omitting everything that would not be necessary to a compact and effective next action, even if that questions or defers dealing with what earlier was thought to be requirement. This concept of minimalism is like the idea of Bellman's Dynamic Programming in control theory [BK60] which breaks down a difficult problem into more tractable steps, except that it applies to our original thoughts rather than to the process rules of an artificial control mechanism.
A Need for Local Models.
It is common in the physical sciences to try to start working from a causally deterministic model, but when systems are complex this determinism takes on an illusory or trivial sense; we are often in reality not in charge of the necessary information to vindicate the use of the deterministic model in anything but tangential and limited ways. Expressing this in terms of mappings following the style of Koichiro Matsuno ref [Mat89], it is fruitless and even misleading to use a one-to-one mapping as a model of the steps of causation when we know no more than enough to make one-to-many or many-to-one models. Those statements which we hear in defence of one-to-one causal mappings of the form "If we could make an indefinite number of observations then......" just do not apply when our primary objective is to make very few or even the fewest possible number of observations. Through its reliance upon precise conditions the one-to-one model is excessively restrictive, and if used over zealously often leads to conclusions which are misleading extreme cases of the more general forms of models.
In the case of using highly refined models which have well defined internal form such as mathematical symbolism, an equivalent issue arises in connection with how we apply these existing formal analyses to the reality. If we cling to the Platonic penchant for fundamental forms we are likely to over estimate the value of formal models, especially standard ones, due to their ready made inherent elegance (not to mention their cultural acceptability). It is vital to enlist another Platonic idea, that of dialectic, in order to bring an equal amount of concern for relevance into the picture and to promote adaptation (refer for example to Plato, Phaedrus 265 and 266 [Pla]).
..... in both Humans and Machines.
At the heart of a process of dialectic there is a continual revival of contention, and it is the live ability to resolve contention which gives the process its special power.
When we apply these ideas to the field of neural networks there emerges a sense of similarity between the processes in the mind of the designer and those in the system being designed. Thus certain models in this area serve to illuminate both of these areas. We seek here to find machine structure which supports such a live contention process within itself whilst limiting commitment of either the machine or its parts in specific ways to the resulting emerging resolutions of the process.
Weaknesses of the Global Viewpoint.
It is still almost universally true that the analysis of a self organising system starts with a global state description. We are concerned in this subject with emergent macroscopic properties in a domain where the detailed process is so complex that uncertainties of structure will usually remain present throughout operation of a system. To attempt the use of a global causal model in such a case is rather like starting the aerodynamics of an aerofoil from the statement of the Navier Stokes laws for general fluid motion. We need models with more layers available so that concerns may be kept better localised. There is nothing wrong with the global model as a general statement and it is useful in handling problems in certain specific classes, but aeroplanes and turbines have been working for a long time, and it is to this day still impractical to lead anybody to an understanding and control of the design of a foil in general by means of deductions from the Navier Stokes equations. For the design of artificial neural networks we also need relevant models.
There is a broad design technique available to avoid relying upon global models, and it is minimalist in style. It is to replace the conventional concern in design for a structure and a content with a concern for synthetic media (as means to structure) and classes of operations (as generalised content). With adequate means of synthesis and analysis of these two things to hand it is possible to assemble machinery with relative ease, and also to satisfy specific patterns of need. In adaptive systems this technique will need to be developed in two or more layers, at least one concerned with the operation as its content and another with the adaptation as its content. However, whereas the implementation of a system would benefit from the maintenance of that division, the design concerns of a physical neuron, as it is commonly thought of, seem to span these two layers. We need to design the medium rather than its application.
To some extent all work on artificial neural networks is already concerned with media and abstract operations, but the degree to which this removal from the specific is driven must be suited to the task in hand. It is a design choice, even a discipline, to keep the development of structure and content apart in this way, and for artificial neural networks it can be taken further yet.
Principal Components Analysis (PCA also known as Karhunen Loéve expansion, see Haykin's book [Hay94] section 9.5) is an optimisation of a linear filter in a similar class to Kalman-Bucy and Wiener/Hopf/Kolmogorov filtering. Such filtering schemes are very limited in handling, let alone in spontaneously learning how to decode, coding created by either non-linear processes or by groups of incoherent sub-processes. Unfortunately in the utterly general case of non-linearity, every other form of prescribed approach to decoding will also fail. But more significantly these linear filters optimised against global criteria cannot even capture the important case of quasi-linear signal mappings occurring independently in arbitrary localities of signal space (i.e. independent subspace mappings with locally smooth properties). They are referred to a canonical framework in the space of the input signal, albeit one derived from the data itself, and cannot adjust to take advantage of features of signals other than global features. This weakness spoils the performance of the system in real work by wasting opportunities for finding relevant structure. It also takes away an opportunity for the designer to treat separately the characterisation by behaviour and performance of the different sets of input signals which might need to be distinguished, and thus it complicates the design process in this respect.
Self referential ways of factorising the signal are required. PCA identifies a hierarchy which is derived from the given signal ensemble, and in that sense it is self referential, but the reference is to the structure of the entire ensemble, not to any localised terms or features within it. This makes it inefficient in handling independently coded source components. The inherent fixed hierarchical form limits its application largely to signals created from a coherently structured source.
In real world signals it is commonplace for independent coding processes to share a common transmission channel. Indeed this is important as a zero protocol method which is essential for simple independent processes to operate communally. The key ingredient which makes this possible has generally two parts. It consists of:
|
a) redundant use of the code space, because this can produce a statistical form of near orthogonality sufficient to avoid ambiguity (cocktail party coding), and b) restriction to either one at a time, or, depending upon degree of redundancy and power of receiver processing, to a very few simultaneous independent transmissions on the common channel. |
Such redundancy appears in natural systems in the animal domain, consider bird song for instance, but it also effectively operates in the domain of human observation and measurement because wherever a natural influence is not sufficiently redundantly signalled by chance then it is impossible for our instruments to separate it from interference. This is such an important class of coding method that it needs special attention.
Unsupervised learning can be used to identify approximately the statistically independent components in many of such composite signal ensembles. Also as far as work on artificial neural networks is concerned a special benefit arises when this capability exists throughout a network because then utterly simple protocols of combining partially formed signals with statistically unrelated codes by either simple addition or by aggregation of separate vectors into larger ones can be used.
We are dealing with the problem of partitioning the independently active cluster regions of a strongly non-Gaussian distribution of frequencies of occurrence in the signal space, for that is the nature of sufficient redundancy. This demands that independent analyses be localised in self identifying separate regions of the signal space. Rather than the hierarchical definition of a polynomial found in Principal Components Analysis, for this to be possible we need to work with more general and non-hierarchical signal subsets as our basis of analysis.
Principal Components Analysis does not, of itself, quantise, or even "soft quantise" (i.e. adjust transmitted signals towards discrete values). Thus it is at best only part of a symbol forming process, and in fact a rather limited case of that. Yet it is commonly believed and stated that PCA is inherently an optimum form of coding, and this is misleading (For explanation of PCA in the form referred to as the Generalised Hebbian Algorithm see [Hay94] section 9.7). Certain arrangements of linear Hebbian neurons can indeed be proved to be optimum in the sense of eigen-vector extraction, but of course, that proof is limited by the same sort of assumptions based in conventional global models and is not sensitive to local signal space relevance. This is an example of a dangerously powerful argument based on a conventional and too global model, dangerous because it so easily hides the emerging possibilities for design.
Limitation of synaptic weights in positively adaptive Hebbian neurons is necessary, but when it is implemented by the direct means of saturation at the synaptic weight registers it has the effect of cross coupling and reducing the gain in the various modes of adaptation, even when the corresponding input signals do not occur simultaneously by addition in the input vector. If instead excessive positive adaptation is moderated by making the adaptive feedback nonlinear then at least for important classes of signals these undesirable effects can be brought under control. Strong nonlinearity can be used in this way in the adaptive feedback path without destroying the linearity of the operational signal paths of the neuron and without cross coupling the signal space localised modes of adaptive action.
This point is not overtly a question of global view but rather one of insufficient abstraction. It deals with the weakness of associating local issues in signal space with exclusive physical regions in the machine structure. The use of physical mappings goes part way to dealing with the problem of uncoupling the handling of the separate regions of the signal space, but it would be better to make individual local issues in signal space remain substantially distributed in machine physical space so that statistical averages may be used as a basis of design.
Notice how Kohonen in his neural networks called "feature nets" (for explanation see section 10.5 in [Hay94]) makes his coding space congruent with the physical space. We know that natural networks show this sort of localisation of functional specialisation in general, but not necessarily to the level of associating specific signals with individual axons. That is a presumption regarding all but the simplest of natural networks, and for design purposes such a restriction is likely to debar other valuable models and mechanisms.
Self Organising Feature Maps and the Linde-Buzo-Gray algorithm perform quantised coding (vector quantising through nonlinearity in the adaptive feedback path) but apart from SOFM using a 2-space topology of association (not really the same thing) they fail to factorise their output code space in the sense that output signals are encoded more or less as one-of-n rather than by a parallel vector expression.
In spite of the conflicting need for it to be quantised, or at least soft quantised, we need to factorise the axonal vector output space in order to gain the possibility of partitioning by context in signal space and then using correlative averaging effects of redundant parallelism to smooth out the discontinuities of the overall mapping.
Over the past couple of decades it has been interesting, if frustrating, to watch the attitudes taken to extension of notions of quantity of information beyond one which is objective and thereby free from interpretive uncertainties. There has been much written and said to defend this absolute sense, yet gradually the signs are appearing that some sort of relativity has to be introduced. I am thinking here of the Shannon sorts of measures, but there has also been plenty of confusion and battle over the separate domain of pure discrete valued representations which are now coming to be called Kolmogorov complexity theory (refer [LV93]). Shannon himself started out by avoiding the relativities by means of isolating his problem to the domain of a channel (or equivalently an experiment), with transmitter and receiver being conceived under an objective framework. If we consider even just the receiver as having uncertainty in its structure then Shannon entropy seems immediately less of an absolute measure, and yet this uncertainty is often present to some extent in real communications problems, and will usually be there in systems of adaptive components.
To apply the notion of entropy to a probabilistically defined class of signals and their channels (rather than just to probabilistically defined signals of one class in one channel) we can determine at best a probability distribution of the entropy values. Along this road we may in the end have to integrate the distribution in ways which are dependent upon the specific conditions of operation. This leads to entropy becoming a multi-dimensional, even infinite dimensional, function of other parameters, and the traditionally concise and invariant nature of entropy is then lost.
It looks as though the idea of entropy is better reserved for use under the relatively stable frames of reference of implementation work, and for no more than examples in the architectural design of a neuron.
It is necessary to retreat somewhat from the habitual quest for global frames of objective reference and find ways of making useful characterisation of mechanisms which can form parts of larger systems but at a level which is sufficiently local to allow grasp by the human mind.
Many people of the determinist bent would attempt to use this list of weaknesses as the means to converge on a solution by combatting each weakness in turn .... a deductive process. However that is not what is attempted here. Instead we make a divergent step at this point. It will mean taking a pause in the line of the argument in which to propose and define the terms of a class of solutions. The class would be very difficult to arrive at from conventional models by means of deductive steps. Such an argument would at least have to use forward or circular references. Nor does the argument claim to be general so much as minimalist. The process is more like cutting a clearing in a jungle.
Deduction alone is not enough.
The matter of trying to educe something is involved in both the way we think of this next step to a particular neuronal architecture, and also in the mechanical function required under that architecture.
We start with a proposal for a pair of concepts:
a) A class of neurons which we might call "Moderated Hebbian".
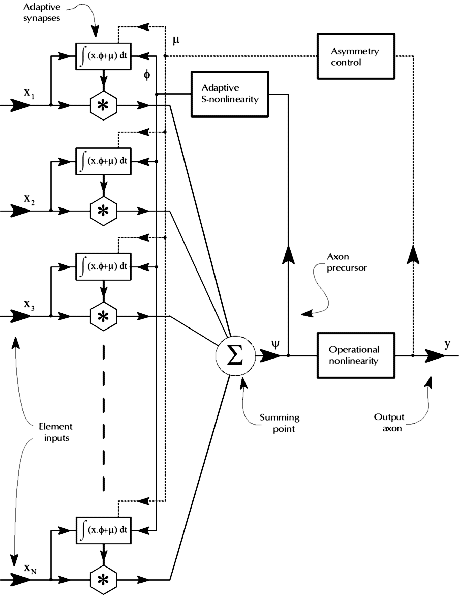
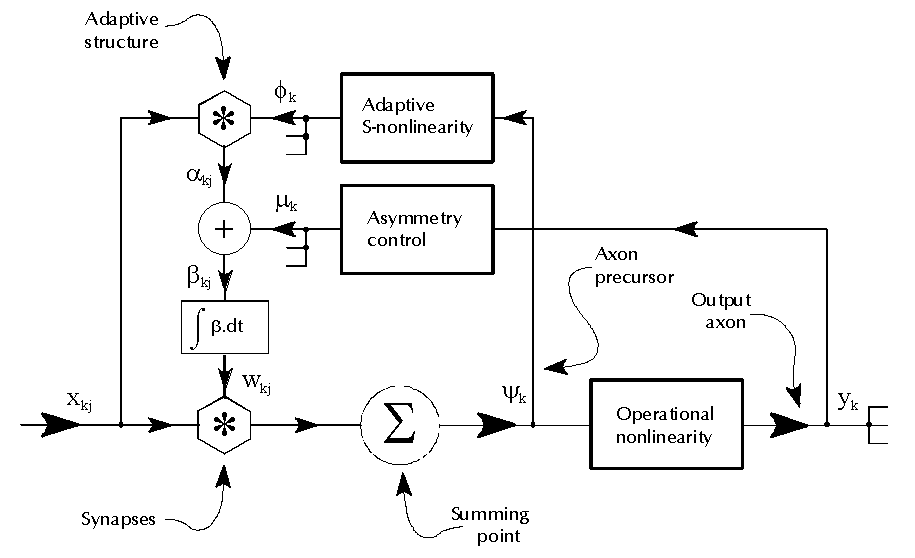
| The diagram F1 shows the signal flow scheme of a neuron. This is a conventional sort but it has strong nonlinearity via an S-shaped function in the feedback path controlling adaptation. This has the effect of causing the synaptic sum (called here the axon precursor) to seek to converge upon moderate non zero values. This maintains the synaptic weights in a moderately dispersed Gaussian distribution without any nonlinear operations applied to the synaptic weight registers individually. An independent nonlinear transmission function, the "operational" nonlinearity, is applied in the path carrying the precursor to the axon output signal proper. |
b) A class of signal ensembles which we might call "Sparse Combinations".
| We define a certain class of signal ensembles as built up of sparse linear combinations from a large set of element signals. With ensembles from this class the behaviour of the Moderated Hebbian type of neuron may be analysed and predicted on a basis that is localised in signal space. It is possible both to characterise a wide range of real world signals and to synthesise useful engineering signals in terms of this class of signal ensembles. |
We may now develop these two concepts in a little more detail.
The neuron signal flow form is shown in diagram F1.

|
The synaptic array is typical of the most usual sorts of artificial neurons
under study. In fact from the point of view of realisation the synaptic
structures are simpler than some because they are entirely linear except for
the two essential multiplication operations, one for signal weighting and the
other for Hebbian adaptive adjustment. The main distinguishing feature
is the use of a strongly nonlinear transmission from the axon precursor to the
common variable controlling adaptive action in the array of synapses.
There are a number of different forms that may be used for this nonliniarity
but the one considered here is that required to give the neuron a binary
resolver characteristic. In that case the nonlinear function is a
symmetrical S-shape with three zeros at say -1, 0 and +1. A typical form
for this function using ka as an adaptive gain parameter is:
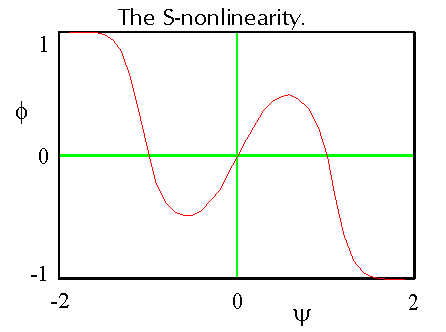
|
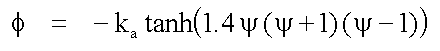
|
The effect of using this form of adaptive control is to make those terms which produce small output at the axon precursor grow larger (positive Hebb adaptation) under competition for synaptic weight variance, whilst those exceeding the required "moderate" symbolic signalling level for the output tend to grow smaller (negative Hebb adaptation), thereby conserving synaptic weight variance.
Notice that this scheme of adaptation uses variance in the weighting array
only sufficient to align the precursor value with the nearer of two attractor
points. Given a distribution of the precursor which is natural to the
signal ensemble and starting from a random state of the synaptic array, this
determines an average variance in the weighting array to adjust ideally any
single degree of freedom in this simultaneous adaptive solution of only about
0.4 times as much as would be the case for supervised training to a specific
pattern. This ratio is approximated by the following expression:
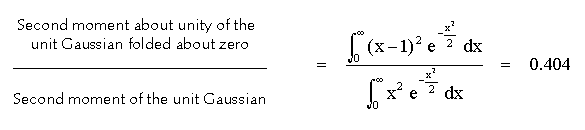
In this way the scheme of adaptation benefits from inherent structure of the signal ensemble, and each neuron can do this so long as it maps a statistically independent linear projection of the signal vector.
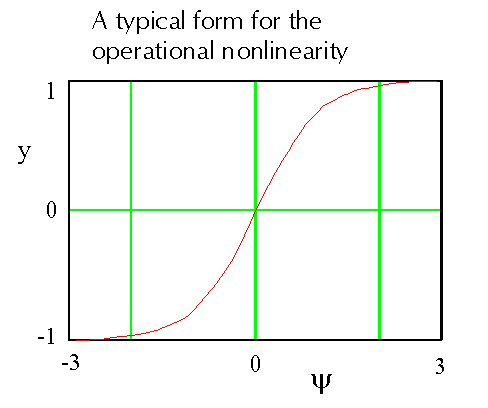
The nonlinearity used in the output path from the axon precursor to the axon
itself may be chosen independently to produce soft or hard quantisation
effects. For the case of a symmetrical binary resolver, which is the
example discussed here, it would typically be a soft saturating function with
a linear region about the origin, which is of the nature of the hyperbolic
tangent function:
|
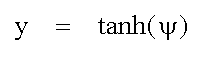
|
A further feedback term is needed to manage the asymmetry of the distribution of the axon precursor signal. For many purposes this need only be a weak signal and in any case will normally produce a null average for the case of a symmetrical resolver type of neuron. Therefore though useful in a model or simulation, to a first approximation its effect may be neglected in analysis.
There is an important class of real world signal ensembles which, by virtue of certain types of information redundancy in their form, may be analysed well in terms of linear combinations of small groups from a large fixed set of arbitrary element vectors, and with further restriction as to which combinations are permitted. Such signal ensembles can be viewed in linguistic terms as having a homogeneous linear combinatorial type of syntax with a large lexicon (collection of words) in which the words (vectors) are not necessarily orthogonal in their signal space, and with:
|
a) defined sub-lexicons determining which elements may occur in combination, and b) restrictions on how many words are likely to occur in combination. |
The restriction b) is not an essential feature of the structure since it can be expressed through sufficiently detailed definition of the lexicons, but it is convenient.
Notice also that the sets of words in these sub-lexicons can overlap to form continuous sets of sets with complex topologies of their signal sub-space boundary connectivities.
This class of signal ensembles contains as a sub-class the shorter truncated cases of principal component polynomial expansions over a linear vector space. However this is a weak example of the species in practical terms because the size (cardinality) of the overall lexicon is then that of a single sub-lexicon whereas in the general case the overall lexicon size is allowed to exceed not only that of any sub-lexicon but in practice even the dimensional order of the vector space by several-fold.
For these "sparse combination" sorts of signal ensembles strong nonlinearity in the adaptation path does not have such deleterious effect in terms of adaptive modal cross modulation as would be the case for a signal ensemble involving general or random linear mixing of a basis vector set spanning the input vector space. So for this important class of input signals:
|
a) The temporal averaging available in practical slow self organising adaptation can be used to enhance rejection of uncorrelated cross modulation noise in the process of adaptation. b) The coherent spacial aggregation of parallel axonal operational signals can be used to achieve correlative rejection of the spacial cross modulation noise introduced by axonal nonlinearity used for soft quantisation. |
This is a richly structured class of signal ensemble characterisations, perhaps in some ways too rich, but it does deal with the representation of terms separable as though arising from incoherent subsystems in the signal source, and many of the forms of ensemble so described can be assessed in terms of how they would be processed by arrays of the Moderated Hebbian type of neuron. Our problem is to break down real signal source cases into this type of characterisation, and it appears that the techniques for doing this are likely to be different for the different sorts of signal source.
A simple sub-class of Sparse Combinations is the one in which a number of different discrete, and not necessarily orthogonal, vectors occur, each in isolation, with a fixed stationary probability distribution of frequency of the different vectors, and possibly accompanied by an additive random vector noise. This corresponds to the case where the sub-lexicons each contain one word, and the lexicon is just the aggregate of all the possible discrete words. Notice that this sub-class does not address any issue of continuous sets in the signal space, and this makes it easier to deal with conceptually.
A sub-class of Sparse Combinations with continuous form corresponds to the pixel vectors of a small area of image. For a simple case consider just black and white, for which all possible forms of a corner figure may appear. If the corner is restricted to being sharp then the set of signals is locally continuous in four or less dimensions, and if a separate factor of softening of the corner is permitted then the space of images can become five dimensional locally. Assessment of the number of orthogonally independent but adjoining sub regions of this overall set of signal vectors for say a ten by ten array of one hundred pixels is an interesting problem. It appears that an array of a Moderated Hebb type of neuron could encode such a set. Linguistically this case amounts to a single lexicon because there are no independent sub-processes envisaged. However it is not difficult to conceive of more subtle cases such as superposition of grey scale images.
Using these notions it is now possible to return to a convergent style of argument for subordinate parts of the development.
Opportunities for New Synthetic Structures.
Here are a number of issues which might be considered to bear upon the choice of structure of the neuron, some of which have received attention elsewhere, but which are concerned with what is required in a self adaptive unsupervised learning neuron if it is to allow partitioning and localisation in the abstractions we use to describe it.
This point is not peculiar to this particular argument, but is important to recognise as a constraint on design of physical neurons. It is that linear mapping is thermodynamically cheap and minimal in its class of elements. The element is the scalar variable transmittance, though by analogy to phase holograms and Fresnel plates, the variable phase transmittance with a unit magnitude complex pair value is also candidate as a simple element. Elements such as these are either of the essentially lossless type where reactive structure controls the coupling, or of the passive linear energy absorbing type where a variable resistance to flow is the basis of control. In either case, there is no need at the synaptic element level for either non-linearity or amplification in handling operational signals. This is important because both of these functions have inescapable energy costs in overcoming a conduction barrier exceeding the ambient thermal energy level of the flow carriers. In ultimate terms of economy of physical realisation this makes the linear mapping fundamental as a primary building element in the most prolific substructures, namely the synapses. The energy/entropy costing parts of the system are then reserved for application in quantities only of the order of the neuron count, not of the much greater synapse count.
The range of elemental structures applicable in the synthesis of artificial neural networks is great compared say with von Neuman computing, and even when compared with combinatorial synthetic logic nets. Therefore the use of a single category called "neural networks" creates an illusion of a single common form of modelling. Seen up close this domain is so rich as to encompass models of information processing which might better be clearly distinguished from one another as specific technologies with separate models.
Nonlinearity in the adaptive loop does not intermodulate operational signals (axon nonlinearity is independent from the adaptive feedback nonlinearity), and has limited intermodulation effects upon adaptation itself so long as there is a form of signal coding which is restricted to sufficiently few simultaneous incoherent terms in combination.
Consider the use of non-linearity in the operational signal paths (not the adaptive mechanisms) of a neural net. A first general appraisal of neuron function usually concentrates on a linear weighted sum operation so that only linear transformations of the operational signals are considered. Then it is often the practice to consider using a discriminator or hard threshold detector as the basis for deriving the axon output signal from the linear sum within the neuron. If we consider as an intermediate to these two extremes the use of transmission functions which are only moderately and smoothly distorted from a linear form then marginal forms of nonlinear mapping become possible without total loss of the proximity and small signal superposition effects which would be present with linear operation.
The signal distortion and intermodulation of incoherent terms caused by a sufficiently smooth or "soft" nonlinearity can be arranged not to dominate the signal, and, particularly for intermodulation between independent signals, they can often be arranged to be incoherent in the vector output of a parallel array of neurons. By this means parallelism used with soft nonlinearity can provide means for designing a balance in common signal paths between the conflicting needs to resolve signals into signal space clusters and to maintain the original terms of multiple signals. Also, to the limited degree of a very few simultaneous uncorrelated signals even superposition of independent signal terms can be handled by this means without complete mutual destruction of the terms.
The use of soft quantisation in successive stages of a network can be designed to produce a focusing effect of signal vector manifolds onto attractors determined by the local adaptive nonlinear feedback in each neuron. Because these focusing transformations are partial they demand less contribution of variance from each stage than would be the case for simultaneous exact mapping (hard attractors), and hence the number of independent mappings of this sort which can be performed under a common adaptation exceeds the linear dimensional limit of the neuron synaptic mapping.
It is true that the nature of dimensional limitations in mappings means that no single mapping (single neuron) can reject random noise alone whether its mechanisms be linear, soft nonlinear or hard nonlinear. However by the use of non-canonical frames of mapping, that is ones with useful but arbitrarily different forms of signal space partitioning of local smooth mapping, this problem which cannot be solved in a scalar output can be handled in the vector space of multiple scalar axonal outputs. This is because the correlative behaviour of large populations can be used to suppress systematically a moderate level of distributed incoherent form.
The usefulness of this may be grasped in the following way. The disruptive discontinuities between localised areas of useful smooth mapping occur with random distribution over the signal space. Thus they have an intensity of correlation degrading effects which can be overcome by means of the coherent effects of a sufficiently large number of parallel signals (axons). The basis of this possibility is that the number of discontinuities needed is related to (actually much less than) the number of signal points to be encoded, whereas the opportunity for distribution of discontinuities of mapping is related to the exponential function of the order of parallelism which is the entire expressible output signal space. Rough calculations indicate that these effects are likely to be useful in practical design work with parallelism from about fifty axons upwards. Above a few hundred axons in parallel the effect is strong enough that it is likely to be better to divide the signal into more groups and to use these in some form of factorisation or redundant expression of the overall coding.
The simple saturation of synaptic weights as is sometimes used to limit positive Hebbian adaptation would seem to offer a sort of granular locking mechanism in the adaptation process, except that the possibility remains for odd synapses to drift off of saturation; it has no hysteresis, only a friction related to the degree of excess stress of adaptation which is driving the weights against their limits. By comparison the use of nonlinear adaptation to create attractors in the domain of the axon precursor signals does not require excess stress of adaptive drive, and it does display hysteresis. For a given signal such a mapping will maintain its drift towards any given attractor until it passes some critical distance towards a neighbouring attractor, at which point it will assume a new allegiance, and start to drift towards the new nearest attractor. This is by nature a form of Coulomb friction (hysteresis) which appears in the mappings of the individual signal species. The number of such hysteretic attractors available to a given signal vector is the number of attractors maintained by the individual neuron raised to the power of the number of neurons acting in parallel (Note: This needs an adjustment based upon entropy if the attractor states within each neuron are non-uniformly occupied). For a symmetrical binary resolver neuron the two attractors in each axon precursor yield a uniform density of attractors in the output vector space at the apices of a hypercube of order equal to that of the output vector.
This type of hysteresis acts differently for different signals according to their respective frequencies of occurrence relative to the whole signal ensemble. For the more frequently occurring signal vectors the hysteresis is strong and so these signals are least likely to suffer disturbance of their output code due to adaptive interactions with other signal species. In simulations of the moderated Hebbian neuron operating with a signal ensemble cardinality substantially exceeding the synaptic vector order (i.e. exceeding the dimensional order of the linear mapping) there is observable a continuous flux of changes of the mappings of the weakest resolved signal vectors, whilst the majority which are strong ones remain locked near to the attractors with a consequent hysteretic effect (A simple simulation of these processes is reported in [Boo89]). If the signal ensemble is reduced in size below the synaptic vector dimensional order then a static result of adaptation comes about, and the hysteresis is then strong for all of this smaller set of signal vectors.
|
Analysis of the Neuron Model.
We may characterise the coding distribution of a single species of neuron input vector in terms of its appearance at the axon precursor, that is as the linear synaptic weighted sum before any downstream nonlinear operations. The relative frequency of occurrence of the species as a fraction of the overall adaptive activity in the neuron is required as a parameter for this characterisation because species with different frequencies will suffer differing degrees of dispersive disturbance to their respective distributions. The parameter kb is used for this, being the ratio of the overall mean rate of adaptive action per degree of freedom of the synaptic adaptation space of the neuron due to its whole input signal ensemble divided by the rate of adaptive action associated with the input signal species in question.
Notice that this does not attempt to form an overall model of the performance of a neuron (let alone either a parallel cluster or a network of them) nor of its synaptic weightings. Rather we want to characterise by probabilistic estimation of a distribution how well a neuron will encode a statistically independent single species of input vector which is presented in the ensemble of input signals. Our particular species is characterised in this sense only as temporally correlatively independent (not necessarily spacially orthogonal) from the others in the ensemble, and having some level of intensity in terms of kb which determines its fraction of the total adaptive impulse being applied to the neuron.
A Markov process model of progressive state change can be established for the way in which the axonal precursor probability distribution p(ψ) evolves for any particular incoherently coded species of neuron input vector as adaptive action proceeds. The state of this process is of infinite dimensional order because we are thinking of it as a probability distribution over a continuous variate of axon precursor values. Written as a differential equation this has the Fokker-Planck form for a statistical variate with one dimension.
The general form of this model is rather close to being a special case of that proposed by Bellman and Kalaba for the adaptive version of their Dynamic Programming [BK60]. However, they do not include the active contention process distributed across the signal space between competing quantised output signals. Their model does not allow the discrete attractor optimisation goals to self determine beneficially. Although this contention process might seem to add to the complexity of the system, it does in fact simplify it for many interesting cases. This is because as the complexity (signal vector order) increases, so the self selection by signal species of their respective output attractors tends towards producing a statistically predictable distribution of interfering disturbances between signals. Unlike any global deterministically conceived approach, biases of the disturbances from unrelated signal species act only as a basis for common coding within each neuron, thus improving the economy. It is only necessary that this bias shall not lead to convergent correlation of mappings between members of the parallel array of neurons.
For a mathematical outline of the Fokker-Planck and Langevin equations refer to Appendix D of [Hay94]. However, although Haykin's book applies them to the analysis of neural nets, it does so only in the domain of random distributions of the synaptic weights. In this paper a model is established for the axon precursor distribution of a signal species in the presence of many other species with different distributions. This model is not global across the neuron function. The dynamics of the individual signal species differ and interact in ways qualitatively analogous to the different sized or charged particles in an ionised fluid mixture.
The rate of change of the axon precursor probability density for any given signal species is the sum of two terms, one systematically constructive of the adaptation and the other randomly destructive. The constructive term is controlled by a function g0(ψ), chosen by the designer. This expresses the rate at which adaptive adjustments will cause each probabilistically ocurring value of axon precursor output corresponding to our particular species of neuron input vector to drift to a preferred attractor value; this is therefore the "drift" term in the Fokker-Planck equation.
The destructively adaptive term represents for our particular input vector species the uncorrelated disturbances of its axon precursor output caused by adjustments to the adaptive state for all the other species competing in the same adaptive space. It has a magnitude proportional to the square root of kb − 1 and also to the local curvature of the current probability distribution; this has a dispersive effect and can be referred to as the "diffusion" term of the Fokker-Planck equation. It is not defined for kb < 1. This corresponds to the situation where the ensemble of input vectors has a size (cardinality) less than the dimensional order of the adaptive process (number of synapses in the neuron), and in all but infinitessimally probable cases the process can then converge to exact mappings.
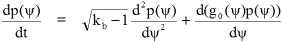 |
This expands to give:
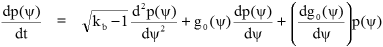 |
To constrain the overall probability to unity it must always be true that:
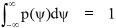 |
and to normalise the ratio of positive and negative adaptive influences:
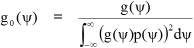 |
We may make an assessment of the long term equilibrium performance in handling a particular species of input vector in the presence of a random pattern of other signal vectors. This is especially interesting where the number of signal points is greater than the order of the neuron input synapse vector, or putting it in terms of the variances or power levels of the respective species of input signals, where the value of kb exceeds 1. Using the Fokker-Planck formula with the dynamic term set to zero leaves the positively adaptive drift term balancing the negatively adaptive diffusion term. This determines the steady state probability distribution function occurring at the axon precursor:
 |
As far as the form of p(ψ) is concerned we can say that when g0(ψ) = 0 then the function p(ψ) is near to a stationary point and its local curvature is:
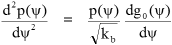 |
and at stationary points of g0(ψ) when 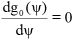 then
then 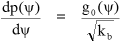
and as 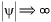 then
then 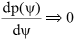
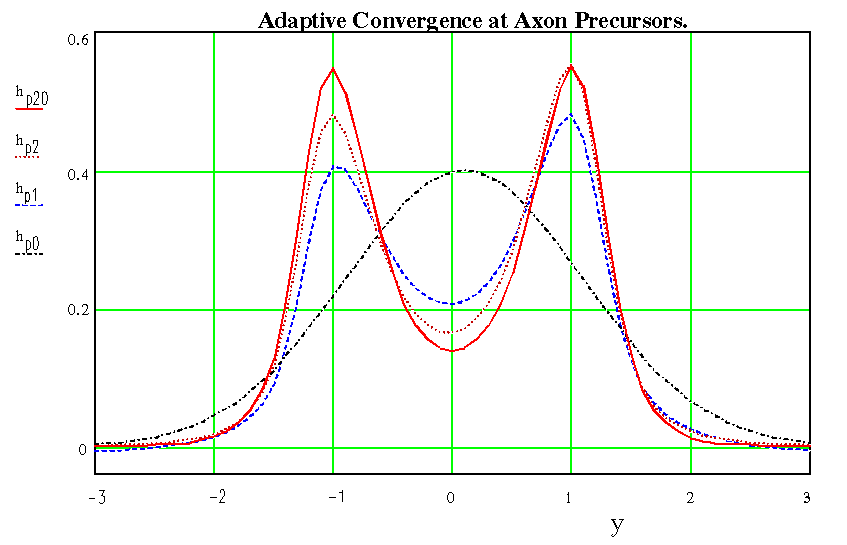
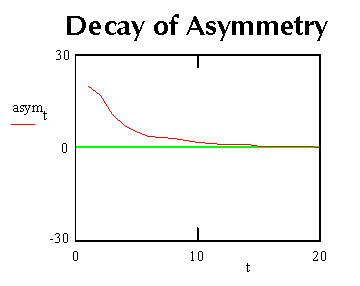
The following graphs show the progress of adaptive change as obtained through
a numerical integration of this equation. It is set up with
kb = 3 (approx.), which is equivalent to studying the behaviour of
one signal amongst an ensemble of similarly weighted signals with three times
as many members as the dimensional order of the synaptic mapping.
|
|
Design Options and Problems of the Neuron.
Using the type of high order moderated Hebbian vector quantisation described here with a level of competitive adaptive activity sufficient to maintain a flux of change of the weakly resolved codes, it appears that there will exist a weak tendency for the dominant principal component to cause a drift of the coding adapted by individual neurons (under non-linear adaptive feedback) towards correlated mappings. Simulations of these sorts of networks have not yet been run long enough to demonstrate this, and it is still possible that for many cases the inherent levels of adaptive state diffusion may obviate such an effect. However it remains possible that for prolonged adaptive operation to be useful it will be necessary to incorporate some form of negative (anti-Hebbian) adaptive lateral links between parallel coding neurons. For this type of network having no hierarchy these links could be randomly distributed, and not forming a directed tree as would be the structure for a network designed for principal components analysis.
Dynamic range of input, or the ability to handle signals by shape and not by
magnitude presents a stark problem to the direct application of nonlinear
processing. The input signals might be brought to roughly standard
levels before substantial cognitive transformation is carried out. The
neuron model discussed here relies upon approximate normalisation of this
sort. However there is hope that an enhanced neuron function could
handle a larger dynamic range so that coding is essentially by shape of
vector, not its magnitude. However this prospect will not be developed
further here.
It might be suggested that anything that can be done by self assignment of symbols within a network can be done, albeit less economically, by a network using only pre-assigned alphabets; after all the economic improvement in utilisation of variance in the synapses through using self assignment amounts to a factor of no more than about 2.5 (see above for the binary resolver neuron). However when the statistical uniformity and freedom of symbol assignment in a randomly inhabited high order signal space are taken into account the value of this technique in the design of large networks becomes clearer.
i) There is a severe management problem involved in any network which has to pull symbols from a stack to assign them for use and to de-assign them when not used (remember this is unsupervised learning).
ii) With a pre-assigned alphabet there is no way of jumping a symbol between adjacent attractors with only slight loss of correlation because there is no such redundancy in the set of permitted codes.
iii) The ability to deploy the working variance in the synaptic array non-uniformly so as to support different mappings with different strengths is hardly possible with a fixed alphabet of output codes, and impossible with an orthogonal alphabet less than or equal in size to the output vector order.
The work leading to this paper was performed on a private basis, and as may be evident from its content, not under the structure of an academic establishment. However I owe acknowledgement to the cyberneticist the late Dr Haneef Fatmi, who was until he died in April 1995 in the Department of Electrical Engineering at King's College London, England. He gave enthusiastic encouragement and discussion in the field of cybernetics embraced in this paper. Also it is a delight to work under the personal advice and guidance, even at a great distance, of Professor Koichiro Matsuno of the Technical University of Nagaoka, Japan. I am very grateful.
[Atm94] W.Atmar "Notes on the Simulation of Evolution."
IEEE Trans Neural Networks V5 N1 Jan 94 pp130-147
[BK60] R.Bellman & R.Kalaba "Dynamic Programming and Adaptive Processes:
Mathematical
Foundation." IRE Trans. Automatic Control Vol. AC-5,1960, pp5-10
[Boo89] A.G.Booth "A Demonstration of Unsupervised Learning in a Model
Neuron."
International Association for Cybernetics 12th International Congress on
Cybernetics
Namur, Belgium. August 1989
[BSM92] A.R.Bulsara, W.C.Schieve & F.E.Moss. "Cooperative Stochastic
Effects in a Model of a
Single Neuron." Published in "Single Neuron Computing" Academic
Press 1992
ISBN 0-12-484815-X Chapter 16 pp503-523
[Has93] M.H.Hassoun. "Associative Neural Memories" Oxford University Press,
New York 1993
ISBN 019-507-6826 £80.00
[Hay94] S.Haykin "Neural Networks: A Comprehensive Foundation." Macmillan/IEEE
Computer
Society Press. 1994 ISBN 0-02-352761-7
[LV93] M.Li & P.Vitanyi "An Introduction to Kolmogorov Complexity and its
Applications."
Texts and Monographs in Computer Science. Springer-Verlag, New York,
1993
ISBN 0-387-94053-7
[Mat89] K.Matsuno "Protobiology: Physical Basis of Biology" CRC Press, Boca
Raton, Florida.
1989. ISBN 0-8493-6403-5
[MV92] H.R. Maturana and F. J. Varela, "The Tree of Knowledge: the Biological
Roots of Human Understanding" (Boston: Shambhala, 1992)
[Pla] Plato "Phaedrus & Letters VII and VIII." Available in english
translation by W.Hamilton in
Penguin Classics.
[VTR91] F.J.Varela, E.Thompson & E.Rosch
"The Embodied Mind: Cognitive Science and Human
Experience." MIT Press, Cambridge MA, USA. ISBN 0-262-22042-3
| Phone and e-mail see foot of AGB home page. | Last updated 9 December 2005 | |
| Back to AGB home page. | Copyright © A.G.Booth 1995-1999 All rights reserved | |